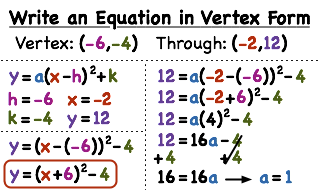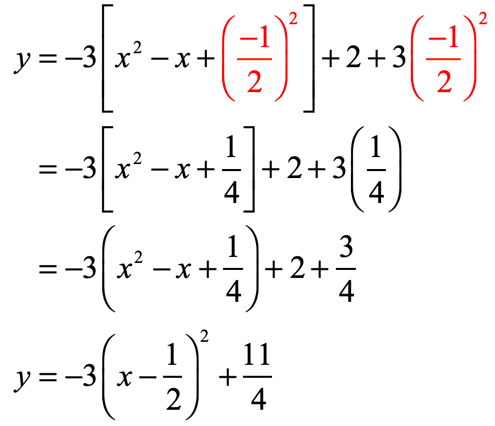H Value In Quadratic Equations

Recognizing characteristics of parabolas.

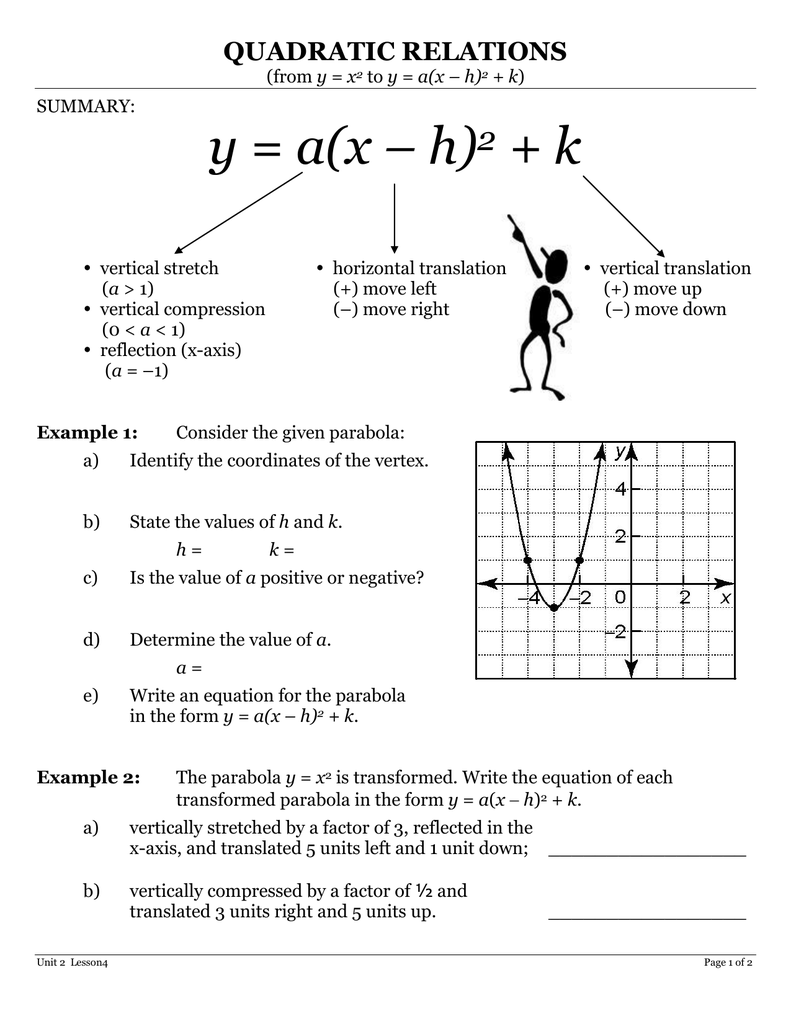
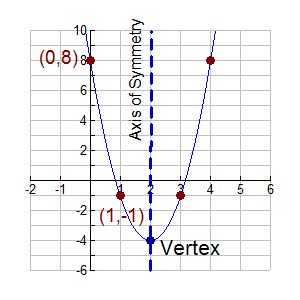
H value in quadratic equations. H b 2a and k ƒ h just compute the h value and plug it into the function to get the k value. The solutions of the quadratic equation are the x x values of the x intercepts. It may be possible to express a quadratic equation ax 2 bx c 0 as a product px q rx s 0 in some cases it is possible by simple inspection to determine values of p q r and s that make. The value of k is the vertical y location of the vertex and h the horizontal x axis value.

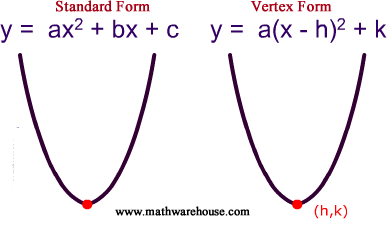
The maximum and minimum value of f occurs at x h. The graph of a quadratic function is a u shaped curve called a parabola. A quadratic equation in standard form a b and c can have any value except that a can t be 0 here is an example. Y a x h 2 k.

The simplest quadratic equation is. Earlier we saw that quadratic equations have 2 1 or 0 solutions. In order to find the maximum or minimum value of quadratic function we have to convert the given quadratic equation in the above form. A quadratic equation with real or complex coefficients has two solutions called roots these two solutions may or may not be distinct and they may or may not be real.

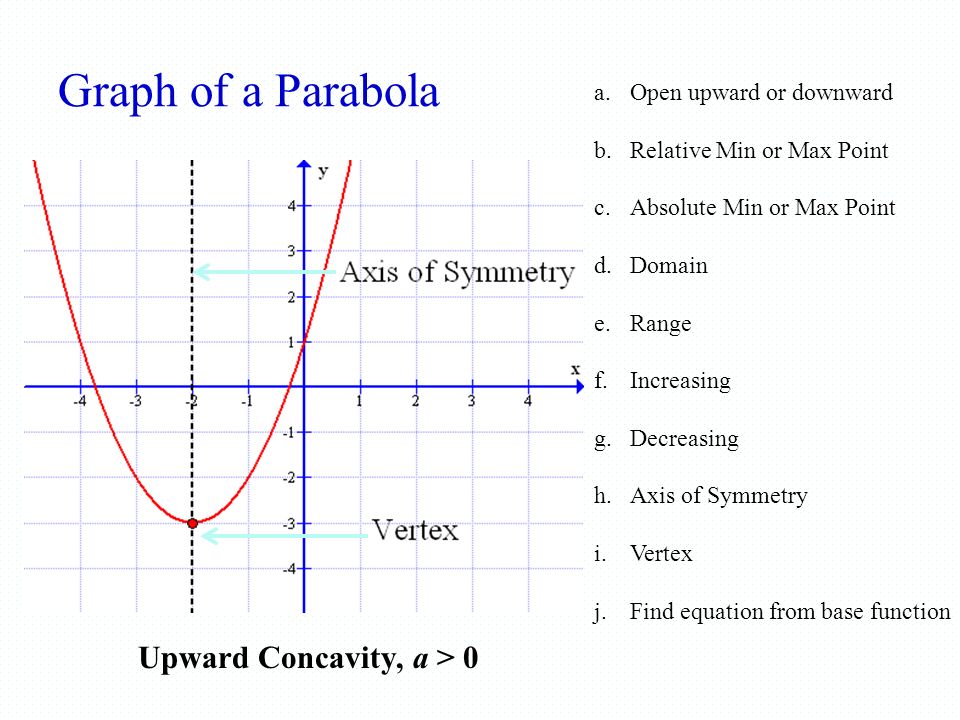
The graph of the quadratic equation f x ax 2 bx c will be either concave upwards a 0 or concave downwards a 0 respectively. Since the solutions of the equations give the x intercepts of the graphs the number of x intercepts is the same as the number of. To find the maximum or minimum value of a quadratic function start with the general form of the function and combine any similar terms. The graphs below show examples of parabolas for these three cases.

To find the minimum value of a quadratic equation we need to understand the nature of the graph of these equations for different values of a. If the parabola is open upward then it will have minimum value. If the parabola opens down the vertex represents the highest point. The standard form of quadratic equation is the equation in form of ax 2 bx c 0.

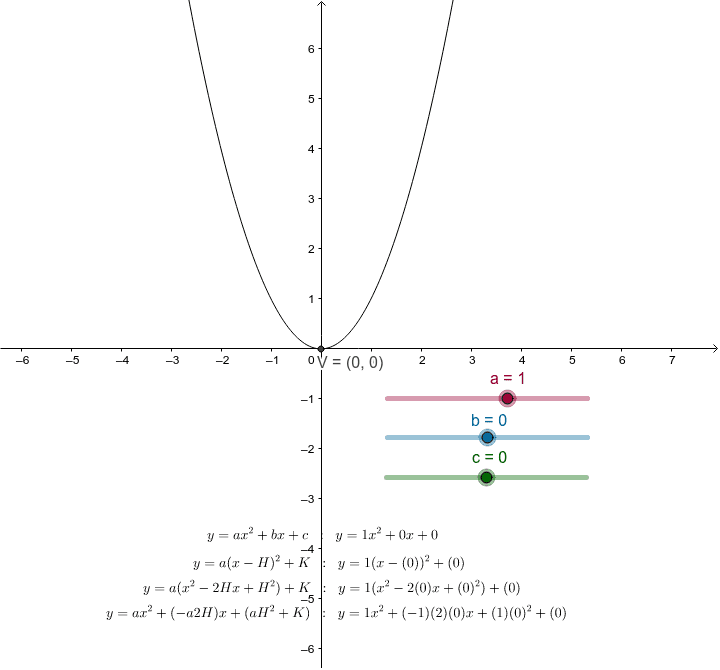
In the graph above click zero under h and k and note how the vertex is now at 0 0. Minimum value of parabola. You can graph a quadratic equation using the function grapher but to really understand what is going on you can make the graph yourself. Here x is the unknown value and a b and c are variables.

But sometimes the quadratic equations might not come in standard form and we might have to expand it. When given the standard form of a quadratic ax 2 bx 2 c you can find the h and k values as. This form of a quadratic is useful when graphing because the vertex location is given directly by the values of h and k.